Prolog

Vor einigen Jahren hockte ich mit einem Freund im Hobbykeller, um uns die Zeit mit unserem gemeinsamen Hobby, der Elektronik, zu vertreiben. Wir bastelten an einem ziemlich verzwickten Problem und schmierten etliche Blätter Papier mit Zahlen und Formeln voll. "Ich hab's", strahlte mein Freund und zeigte mir seinen Ansatz. Ich war skeptisch. "Aber das führt doch zu drei Gleichungen mit drei Unbekannten!" "Macht doch nichts", winkte mein Freund ab, "sowas löst man mit Matrizen. Mit denen kann man alles machen." "Na, dann mach' mal", forderte ich ihn auf. Er wurde verlegen: "Ehrlich gesagt, ich weiß nicht mehr, wie das geht. Aber ich bin sicher, dass das geht." Immerhin etwas, dachte ich und griff zu einem Messgerät, um dem Problem auf praktische Weise zu Leibe zu rücken.

Bis vor kurzem hatte ich von Matrizen nicht die Spur einer Ahnung. Unter Vektoren konnte ich mir wenigstens noch verschwommen etwas vorstellen, aber Matrizen? Dass sie unheimlich leistungsfähig sein sollen, war mir schon zu Ohren gekommen, und in OpenGL redet man ständig von Matrizen, Motivation genug, einige alte Mathebücher hervorzukramen.

Am Anfang ist der Vektor ...

... und am Ende immer noch

Dass Vektoren und Matrizen viel miteinander zu tun haben, wurde mir schnell klar. Dabei musste ich mich jedoch von der Vorstellung, dass Vektoren zwangsläufig etwas Physikalisches oder Geometrisches darstellen, lösen. Vektoren sind Gebilde, die aus mehreren Zahlen bestehen und mit denen man bestimmte Operationen durchführen kann. Das Einführungsbeispiel in einem Mathebuch war drastisch, etwa so ähnlich:

Artikel  Einzelpreis   Menge   Preis

Schlauch       1.95      20    39.00
Ventil         0.35     100    35.00
Mantel         3.70      10    37.00

Summe                         111.00

Einkauf einer Fahrrad-Reparatur-Werkstatt. Der Gesamtpreis wurde als Skalarprodukt verkauft, was ja auch stimmt, wenn man die Einzelpreise als einen Vektor und die Menge als einen zweiten betrachtet. Mal 'ne ganz andere Betrachtungsweise, Skalarprodukt ohne Cosinus. Über den Sinn eines solchen Vorgehens kann man natürlich streiten.

Trotzdem, mitunter kann es ganz hilfreich sein, wenn man sich von allzu starren, einseitigen Vorstellungen löst. Bei Matrizen ist es ähnlich. Sie sind zunächst nicht mehr oder weniger als tabellenartig angeordnete Zahlen, mit denen man bestimmte Operationen durchführen kann. Die Flexibilität von Matrizen wird nicht durch eine Fülle von verschiedenen Operationen erreicht, sondern durch die Vielfalt, mit der man die Tabellen mit sinnvollen Zahlen füllen kann. Operationen gibt es nur wenige, wobei die Multiplikation mit einem Vektor vielleicht die wichtigste ist, so wichtig, dass ich damit den Einstieg in die Matrizenwelt riskieren möchte.

Nehmen wir die folgenden beiden Vektoren, ohne zu fragen, was sie bedeuten, und berechnen das Skalarprodukt:

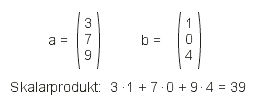
So oder ähnlich wird es üblicherweise dargestellt. Ich versuche es mal mit einer unkonventionellen Darstellung und lege die Vektoren quer:

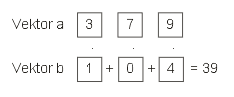
Nun gehen wir hin und multiplizieren den Vektor a zusätzlich mit einem zweiten Vektor:

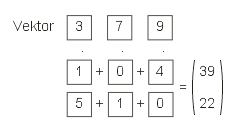
Da haben wir die Matrix. Heraus kommen zwei Zahlen, die wiederum einen Vektor bilden, aber nur mit zwei Komponenten. Wenn wir die Matrix alleine betrachten und so aufschreiben, wie es sich gehört, sieht sie folgendermaßen aus:

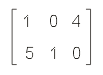
Die Matrix hat, wie unschwer zu erkennen ist, zwei Zeilen und 3 Spalten. Sie kann nur mit 3-stelligen Vektoren multipliziert werden, und heraus kommt ein 2-stelliger Vektor. Es gibt keine Gründe, einzeilige Matrizen zu verbieten, so dass man den Vektor b weiter oben auch schon als Matrix auffassen kann. Im Prinzip kann eine Matrix beliebig viele Spalten und Zeilen haben. Oft ist sie symmetrisch angelegt und hat genau so viele Spalten wie Zeilen. Die OpenGL-Matrix mit 4 x 4 Zahlen gehört dazu. Ist auch logisch, denn das Ergebnis soll von gleicher Art sein wie die "Eingabe".

Ich habe bewusst Zahlenbeispiele genommen, denn die übliche, allgemeine Schreibweise mit zweistelligen Indices ist gleichermaßen korrekt wie unübersichtlich.

Erste Sinngebung

Wenn wir mal von der komischen Rechnung ganz oben absehen, wirkt das alles sehr formal, und es taucht natürlich die Frage auf, wozu das Ganze gut sein soll. Dazu ein simples Beispiel, quasi als Motivation. Ich greife wieder mein eigenes Schema auf:

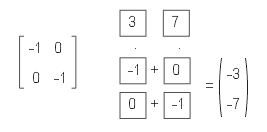
Hier haben wir eine Matrix dazu benutzt, um einen zweistelligen Vektor in die andere Richtung zu verweisen. Wir haben also praktisch den Gegenvektor berechnet. Nun brauchen wir für einen solch simplen Fall keine Matrix, aber das Beispiel soll auch nur andeuten, dass man mit sinnvoll gestalteten Matrizen durchaus Sinnvolles berechnen kann, nicht nur in der Fahrradwerkstatt. Es kommt eben darauf an, die richtigen Zahlen in die Matrix zu schreiben, dann kann die sture, nach Schema-F durchgeführte Vektor-Matrix-Multipliation durchaus eine Menge leisten. Somit wird die Untersuchung, welche Zahlen zu welchen Ergebnissen führen, als nächstes anstehen.