Zurück ins Koordinatensystem

Nach den allgemeinen Betrachtungen begebe ich mich schnell zurück auf das vertraute Terrain der Geometrie mit ihrem anschaulichen Koordinatensystem. Um die Vorstellungskraft nicht unnötig zu strapazieren, begnüge ich mich ferner mit 2 Dimensionen. So kommen wir mit Vektoren aus, die zwei Komponenten (x und y) haben, und die passenden Matrizen bestehen aus 2 x 2 Zahlen.

Distributiv? Aufschlussreiche Zerlegung

Vektoren können wir addieren und multiplizieren, egal, ob das mit Einzelvektoren oder in einer komplexeren Matrix geschieht. Immer, wenn zwei verschiedene Operationen dieser Art anliegen, stürzen sich die Mathematiker darauf und fragen: Ist das Ganze distributiv, so nach dem Motto
n(a + b) = na + nb ? (1)

Auf Vektoren und Matrizen bezogen, lautet die Frage etwa so: Kann ich, anstatt einen Vektor als Ganzes mit einer Matrix zu multiplizieren, den Vektor auch in Teilvektoren zerlegen, diese einzeln mit der Matrix multiplizieren und die Ergebnisse anschließend addieren? Ich will es vorwegnehmen: Ja, man kann und darf, und dabei lassen sich interessante Dinge beobachten. Dazu betrachten wir einen konkreten Vektor und gleich dazu eine Matrix:

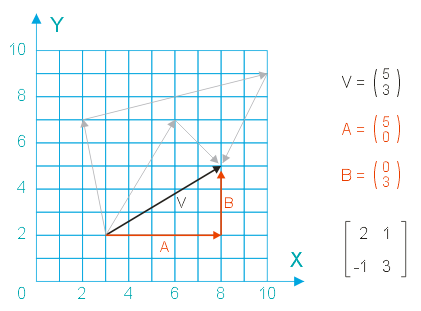
Möglichkeiten, den Vektor in zwei (oder auch mehr) Bestandteile zu zerlegen, gibt es unendlich viele, wie die grauen Pfeile andeuten, doch aufschlussreich ist vor allem die Zerlegung in die Koordinatenvektoren. Das sind Vektoren, die parallel zu den Achsen des Koordinatensystems verlaufen (rot gezeichnet). Die Matrix rechts unten ist willkürlich gewählt; sie soll hauptsächlich eine Kontrollrechnung ermöglichen. Die führen wir nun durch, wobei ich das bekannte Matrixschema wieder aufgreife.

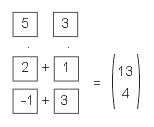Zunächst schicken wir den Gesamtvektor V durch die Matrix und erhalten den neuen Vektor mit den Koordinaten (13; 4).

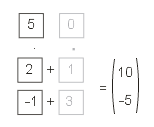Nun der Teilvektor parallel zur x-Achse.

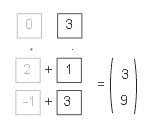Schließlich setzen wir noch den Teilvektor parallel zur y-Achse auf die Matrix an ...

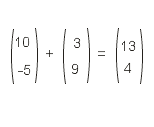... und addieren die beiden mit der Matrix multiplizierten Teilvektoren. Wir sehen, die Rechnung stimmt. Das Beispiel bestätigt, dass Distributivität vorliegt, wenngleich das noch kein Beweis ist. Aber Beweise wollen wir uns sparen.

Wichtig ist eine andere Beobachtung: Für die x-Komponente des Eingangsvektors ist nur die linke Spalte der Matrix zuständig, während die rechte Spalte die y-Komponente bearbeitet. Wir können also die beiden Komponenten getrennt betrachten und die Matrix in "Zuständigkeitsbereiche" aufspalten.

Zerlegung in die Einheiten

Mit dieser Erkenntnis gehen wir noch einen Schritt weiter und zerlegen die Bestandteile des Vektors in Koordinaten-Einheitsvektoren oder auch Basisvektoren. Das sind Vektoren, die nicht nur parallel zu den Achsen des Systems verlaufen, sondern darüber hinaus die Länge 1 haben. Gleichzeitig verschieben wir den Vektor zum Koordinaten-Nullpunkt, um bequemer damit umgehen zu können:

Nun könnten wir sämtliche Teilvektoren durch die Matrix schicken, würden dadurch aber nichts Neues erfahren. Stattdessen betrachten wir nur jeweils einen x- und y-Vektor und prüfen, wie die schon bekannte Matrix darauf wirkt.

Das folgende Bild zeigt noch einmal die Matrix-Mulitplikation mit den Teilvektoren:

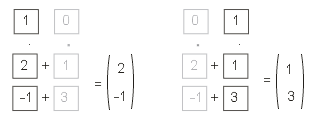
Eigentlich ist der Sachverhalt ja klar, nur sehen und erkennen muss man ihn. Den Spalten der Matrix können wir unmittelbar entnehmen, was mit den Einheitskoordinaten geschieht, wenn wir sie mit der Matrix bearbeiten. Das Koordinatenpaar (1; 0) wird nach (2; -1) verschoben. Entsprechend wird das Koordinatenpaar (0; 1) nach (1; 3) verschoben. Das schauen wir uns mal in der Zeichnung an:

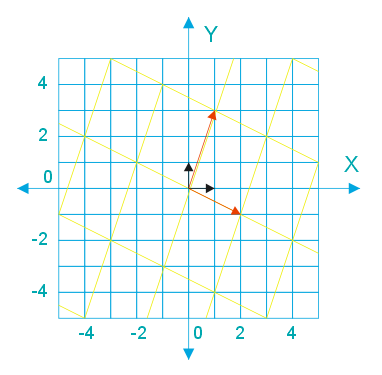
Schwarz sind die beiden Koordinaten-Einheitsvektoren, rot die entsprechenden Vektoren, nachdem sie durch die Matrix gegangen sind. Aber es handelt sich immer noch um Einheitsvektoren, allerdings in einem neuen Koordinatensytem, das in der Zeichnung gelb darüber gelegt wurde. Der Nullpunkt ist natürlich geblieben.

Nun können wir erkennen, was die Matrix macht. Sie rotiert ein wenig nach rechts, verzerrt und skaliert (y mehr als x). Ob es für eine solche Matrix eine sinnvolle Anwendung gibt, sei dahingestellt. Jedenfalls können wir eines festhalten: Wenn wir wissen, was mit den Koordinaten-Einheitsvektoren geschehen soll, können wir auch die Matrix zusammenbasteln, die das für jeden Vektor erledigt. Das wird Thema des nächsten Beitrags sein.

(1) Genau genommen stellen Mathematiker solche Fragen nicht, sie benutzen sie allenfalls, um Schüler zum Nachdenken zu bringen. Nein, Mathematiker legen fest: Das, was ich meine, ist distributiv, und wenn etwas nicht distributiv ist, kann es nicht das sein, was ich meine. Auch 'ne Art, von der Welt mit ihren phantastischen Gesetzmäßigkeiten Besitz zu ergreifen.