Wir rotieren

Im letzten Beitrag haben wir erkannt, wie wichtig die Koordinaten-Einheitsvektor sind, und dass die Veränderungen, wie wir mit ihnen vornehmen, unmittelbar in den Spalten der Matrix erscheinen. Mit diesen Erkenntnissen wollen wir nun gezielt einige Matrizen basteln. Die erste soll Vektoren um 90° nach rechts drehen. Das könnte so aussehen;

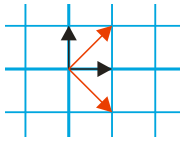
Der x-Einheitsvektor zeigt nicht mehr auf (0; 1), sondern auf (1; -1), während die Spitze des y-Vektors von (0; 1) nach (1; 1) wandert. Und schon haben wir die Matrix, die das erledigt:

Natürlich prüfen wir das nach. Nehmen wir dazu ein Dreieck, dessen Punkte wir durch die Matrix schicken.

Ich denke, die Zeichnung spricht für sich. Die Rechnung will ich hier nicht wiedergeben, sie ist einfach nachzuvollziehen.

Dass hier eine Rotation um 45° nach rechts stattgefunden hat, lässt sich anhand der Lage der Seiten gut nachvollziehen. Zugleich gab es aber eine Skalierung von 1.41, die damit zusammenhängt, dass wir in dem Einheitsquadrat von der Seite auf die Diagonale gegangen sind.

Rotation um einen beliebigen Winkel

Als nächstes wollen wir eine Rotation um einen beliebigen Winkel erreichen, dabei aber auch den Schönheitsfehler der ungewollten Skalierung vermeiden. Wir betrachten jetzt nur die Gegend in der unmittelbaren Nähe des Nullpunktes:

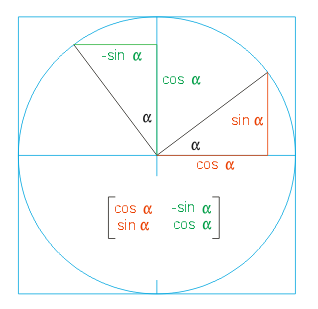Rot sind die neuen Koordinaten des x-Einheitsvektors, gruen die des y-Einheitsvektors.

Der Einheitskreis stellt sicher, dass mit dem Faktor 1 skaliert wird. Bei positivem Winkel alpha erfolgt eine Rotation entgegen dem Uhrzeigersinn. Wir können nun unmittelbar ablesen, welche Winkelfunktionen zu der gewünschten Vektordrehung führen, und wie sich die Werte der Winkelfunktionen in Koordinaten niederschlagen. Die Matrix steht in der unteren Bildhälfte.

In ähnlicher Weise lassen sich weitere Matrizen erstellen. Sehr einfach ist es, Matrizen zum Skalieren zu formulieren, oder Matrizen, die an der x-Achse und/oder der y-Achse spiegeln. Oder eine Identity-Matrix, die nichts macht und die Einheitsvektoren dort belässt, wo sie sich befinden.

Und die Verschiebung?

Bei allen bisherigen Überlegungen blieb der Koordinatennullpunkt unverrückbar an seiner Stelle. Die scheinbar einfachste Operation, nämlich das schlichte, parallele Verschieben, kam in diesen Überlegungen nicht vor. Konnte auch nicht, denn mit den Mitteln eines 2-Komponenten-Vektors bzw. einer 2x2-Matrix lässt sie sich nicht durchführen. Den Grund zeigt folgender Gedankengang: In den 2x2-Matrizen werden alle Komponenten der Vektoren verarbeitet, das heißt, es gibt keinen Summanden, in dem nicht eine Vektor-Komponente als Faktor enthalten ist. Die Verschiebung ist aber unabhängig von den Vektoren; sie ist vergleichbar mit einer additiven Konstanten.

Da bleibt nichts anderes übrig, als in der Matrix eine Spalte hinzuzufügen, die nur für die Verschiebung sorgt. Um die Zahlen für diese Spalte zu finden, brauchen wir nicht den Koordinaten-Einheitsvektor zu bemühen; das geht ohnehin nicht, weil dieser immer auf den Nullpunkt bezogen ist.

Hier übernimmt der Ausgabevektor die x- und y-Werte des Eingabevektors und verschiebt alles um 3 Einheiten in x-Richtung und -2 Einheiten in y-Richtung.
Aber da fehlt noch etwas. Ein Skalarprodukt kann nur gebildet werden, wenn beide Vektoren die gleich Anzahl von Komponenten haben.

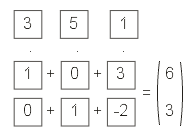Folglich muss auch der Vektor eine zusätzlich Komponente erhalten, nennen wir sie "w". Mit einer 1 an dieser Stelle sorgen wir dafür, dass die in der Matrix vorhandenen Zahlen schlicht und ergreifend addiert werden.

Doch die zusätzliche Komponente ist nicht nur Angleichung an die Matrix, sondern kann ganz nützlich sein. Wenn wir dem Vektor hier eine 0 mit auf den Weg geben, bleibt die letzte Spalte der Matrix unwirksam, es wird nicht verschoben, obwohl die Matrix dazu eingerichtet ist. Der Gedanke lässt sich weiter spinne, denn alle Zahlen sind erlaubt und möglich.

Schließlich sollte die Matrix noch eine dritte Zeile erhalten, damit der Ausgabevektor zum Eingabevektor passt.

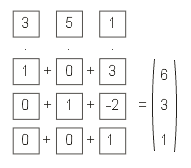In der nebenstehenden Matrix macht die untere Zeile nichts weiter, als dass sie die W-Komponente an den Ausgabevektor weiterreicht.

Ich müsste jetzt noch ein Beispiel präsentieren, aber ich denke, die Sache ist so klar, dass ich darauf verzichten kann. Stattdessen möchte ich noch eine Matrix vorzeigen, die verschiedene Transaktionen enthält. Den Zusammenhang zwischen den Transaktionen will ich (noch) nicht untersuchen, aber auf einige Probleme hinweisen:

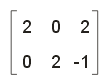Die beiden Zahlen in der rechten Spalte verraten sofort, dass eine Verschiebung von 2 Einheiten in x-Richtung und -1 in y-Richtung stattfinden soll. Die beiden Zweien links davon weisen auf eine schlichte Verdopplung, also eine Skalierung hin

Durch diese Matrix ziehen wir nun das schwarz gezeichnete Dreieck und erhalten das rote:

Hm, die Verdopplung der Größe passt, wie wir durch Abzählen schnell herausfinden können. Auch die Parallelität bleibt erhalten. Aber die Lage irritiert ein wenig. Wenn wir den linken, unteren Punkt des Dreiecks betrachten, dann stellen wir fest, dass sich y trotz Matrix nicht verändert hat.

Der Zusammenhang wird deutlicher, wenn wir das grüne, gestrichelte Dreieck hinzunehmen, das ohne Verschiebung, also nur durch Skalierung entstanden ist (w = 0).

Nun erkennen wir auch die Verschiebung. Es wird folglich erst skaliert, wodurch die einzelnen Punkte eine andere Lage bekommen, und dann wird das Ganze noch einmal verschoben. Die Rechnung stimmt also. Das Beispiel zeigt aber auch, dass kombinierte Aktionen ihre Tücken haben. Wir haben mit diesen Tücken Bekanntschaft gemacht, wenn wir bei glTranslate und glScale oder glRotate nicht die richtige Reihenfolge beachtet haben.