Addition von Matrizen

Der Vollständigkeit halber beginne ich mit der Addition mehrere Matrizen. Addieren lassen sich nur Matrizen mit gleicher Zeilen- und Spaltenanzahl. Dabei werden die ganz einfach die einzelnen Komponenten addiert.

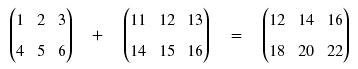
Die Matrizen können bei der Addition vertauscht werden, die Addition ist also kommuntativ. Ferner gilt das Assoziativgesetz; wir können demnach beliebige Teilsummen bilden. Für OpenGL hat die Matrizenaddition keine besondere Bedeutung.

Skalarmultiplikation von Matrizen

Dabei wird eine Matrix mit einer skalaren Zahl multipliziert. Der Vorgang ist recht simpel: Jede Komponente wird mit der Zahl multiplizert. Ähnlich geht es ja auch bei der Verktormultiplikation mit einem Skalar zu.

Multiplikation zweier Matrizen

Die Matrizenmultiplikation spielt in OpenGL eine zentrale Rolle. An dieser Stelle geht es um den formalen Algorithmus, der allerdings nicht ganz einfach zu durchschauen ist und bei größeren Matrizen recht umfangreich wird. Es ist die typische Angelegenheit für eine Funktion, die man einmal programmiert und im folgenden nur noch benutzt. Im übrigen enthalten fast alle mathematischen Funktionssammlungen zu OpenGL entsprechende Funktionen. Das gilt, um es vorwegzunehmen, ebenfalls für die weiter unten zu besprechende Matrix-Vektor-Multiplikation.

Bei der Matrizenmultiplikation wird jede Zeile der einen Matrize mit jeder Spalte der zweiten Matrize ausmultipliziert, und zwar in derselben Weise, wie ein Skalarprodukt gebildet wird. Die Ergebnisse bilden dann wieder eine Matrize, die allerding bezüglich der Zeilen- und Spaltenzahl nicht mit den ursprünglichen Matrizen übereinstimmen muss. Hier ein Zahlenbeispiel:

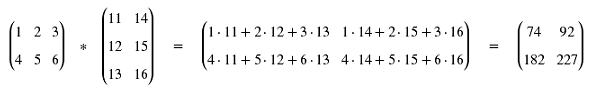
Da man die Zeilen und Spalten einer Matrix auch als Vektoren auffassen kann, lässt sich die Rechenregel deutlich übersichtlicher formulieren. A und B sind die Zeilenvektoren der ersten Matrix, C und D die Spaltenvektoren der zweiten. In der Ergebnismatrix stehen die 4 Skalarprodukte.

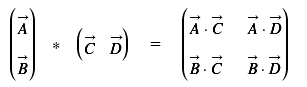
Man sollte sich klar machen, dass beide Matrizen ihre eigenen, unterschiedlichen Auswirkungen auf das Ergebnis haben. Die erste Matrix wird zeilenmäßig ausgewertet und bestimmt damit auch die Anzahl der Zeilen in der Ergebnismatrix. Die zweite Matrix dagegen wird spaltenmäßig ausgewertet und bestimmt die Anzahl der Spalten in der Ergebnismatrix. Da jeweils eine Zeile der ersten Matrix mit einer Spalte der zweiten Matrix komponentenweise verknüpft wird, müssen diese zusammenpassen. Das heißt, ein Zeilenvektor der linken Matrix muss genau so viel Komponenten enthalten wie ein Spaltenvektor der rechten. Anders ausgedrückt: Eine Matrizenoperation ist nur möglich, wenn die Spaltenzahl der linken Matrix gleich der Zeilenzahl der rechten Matrix ist.

Andererseits z.B. die Spaltenzahl der rechten Matrix beliebig. So könnte, um das Beispiel noch einmal aufzugreifen, die rechte Matrix ohne weiteres 3 oder mehr Spalten enthalten ...

Vektor-Matrix-Multiplikation

... oder auch nur eine. Dann haben wir den Sonderfall, dass eine der beiden Matrizen nichts anderes als ein einfacher Vektor ist.

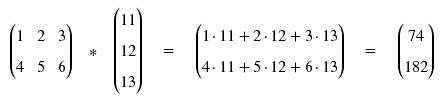
Das Ergebnis ist logischerweise eine einspaltige Matrix, also wieder ein Vektor. Die Rechenregeln sind dieselben wie für die Matrizenmultiplikation allgemein, nur dass in diesem Fall die Sache recht überschaubar ist.

Vektor-Matrix-Multiplikationen spielen ebenfalls in der OpenGL-Praxis eine große Rolle, so dass dafür üblicherweise eine spezielle Funktion bereit gestellt wird.

Matrizenmultiplikation - was geschieht beim Vertauschen?

Es leuchtet nicht unmittelbar ein, warum Matrizen bei der Multiplikation nicht vertauscht werden dürfen. Einige Zahlenbeispiele sollten das aber plausibel machen. Zuerst betrachten wir die Matrizen im obigen Beispiel und vertauschen ihre Rollen:

Es entsteht eine völlig andere Matrix, in diesem Fall sogar mit einer anderen Spalten- und Zeilenzahl als im ersten Beispiel. Doch wie sieht es bei quadratischen Matrizen aus, die ja keine Unverträglichkeiten haben, wenn es um die Zeilen- und Spaltenzahl geht? Nehmen wir als Beispiel eine kleine 2x2-Matrix und vertauschen hier ebenfalls:

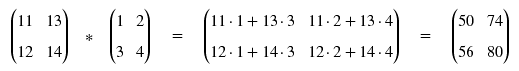
Ich denke, das Ergebnis ist eindeutig.

Transponieren von Matrizen

Hierbei wird die Anordnung der Elemente in der Matrix geändert. Aus den Zeilen werden Spalten oder umgekehrt:

Wir können auch sagen, dass die Matrix an der Diagonalen links-oben rechts-unten gespiegelt wird. Die Elemente tauschen ihre Positionen. Da die Position in einer Matrix eine wesentliche Bedeutung hat, und da diese Positionsänderungen nach einer festen Regel erfolgen, handelt es sich um eine echte Matrixoperation, mit denen bestimmte Probleme gelöst werden können. Abgesehen davon kann es auch nur eine Formalität sein, z.B. wenn eine Programmfunktion die Matrix zeilenmäßig erfasst, eine andere aber spaltenmäßig.