Was ist eine Normale?

Eine Normale ist ein Vektor, der senkrecht auf einem planaren Polygon bzw. einer Ebene steht. Damit bestimmt die Normale eindeutig die Ausrichtung des Polygons.

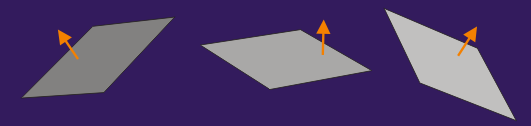
Dieser Vektor ist grundsätzlich normalisiert, hat also die Länge 1 (daher die Bezeichnung). Viele Berechnungen, die mit der Normalen durchgeführt werden, erwarten einen normalisierten Vektor. Außerdem handelt es sich um einen reinen Richtungsvektor, dessen Länge keine Aussagekraft hat.

Normalisieren eines Vektors

Um einen beliebigen Vektor zu normalisieren, muss zunächst seine Länge (Betrag, Skalar) bekannt sein. Der Vektor wird dann durch seine Länge dividiert:

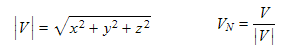
Beispiel: Der Vektor (2, 1, 2) hat die Länge sqrt(4 + 1 + 4) = 3. Die drei Komponenten werden durch 3 dividiert, und das Ergebnis ist der normalisierte Vektor (0.67, 0.33, 0.67).

Funktion zur Normalisierung eines Vektors:

TVector NormalizeVector (const TVector &v) {
    double denom = sqrt (v.x * v.x + v.y * v.y + v.z * v.z);
    // in this term the denominator is always >= 0
    // (division by 0 not possible)
    return ScaleVector (1.0 / denom, v);
}

Ermittlung der Normalen

Bei einem dreieckigen Polygon geht man von einem beliebigen Eckpunkt aus und bestimmt von hier aus die beiden Vektoren zu den anderen Eckpunkten. Das Vektorprodukt (cross product) ist nach anschließender Normalisierung die gesuchte Normale. Damit sie in die richtige Richtung zeigt, werden die beiden Seitenvektoren entgegengesetzt dem Uhrzeigersinn übergeben.

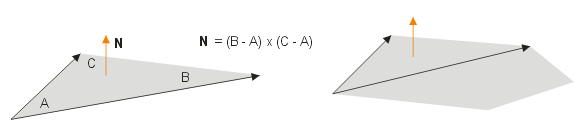
Bei Polygonen mit mehr als drei Ecken verfährt man im Prinzip genau so. Dazu wird lediglich ein Dreieck abgetrennt.

Anwendung von Normalen

Beleuchtung. Damit OpenGL das Licht entsprechend dem Einfallswinkel richtig dosieren kann, muss vor dem Zeichnen des Polygons seine Normale übergeben werden. Das geschieht mit glNormal. Der Befehl kann an beliebiger Stelle stehen, auch innerhalb der Klammer glBegin und glEnd. Die mit glNormal eingestellte Normale ist die aktuelle Normale; sie bleibt wirksam, bis eine andere Normale übergeben wird. - OpenGL erwartet per Default eine "normalisierte Normale". Mit glEnable (GL_NORMALIZE) kann man das Normalisieren jedoch an OpenGL delegieren. In diesem Fall ist die Länge des Vektors beliebig (siehe unten "Normale und Transformationen").

Berechnungen mit Ebenen. Die Normale ist neben einem zusätzlichen Punkt (oder alternativ der Ebenenkonstante) eine Komponente zur Definition von Ebenen. Praktisch alle Berechnungen, die mit Ebenen durchgeführt werden, greifen auf die Normale zurück. Einige Beispiele:

• Positionsbestimmung beim Frustum-Culling. Dazu werden die Normalen der 6 Frustum-Ebenen herangezogen.
• Berechnung der physikalischen Kräfte auf abschüssigem Gelände. Hierbei werden die Normalen der Terrain-Polygone benötigt.
• Kollisionserkennung und -verarbeitung. Kollisionen mit Polygonen sind abhängig vom Aufprallwinkel. Die Normale eines Polygons wird gebraucht, um die Intersektion zu berechen, aber auch - falls erforderlich - den Gleitpfad entlang des Polygons.

Vertexnormale

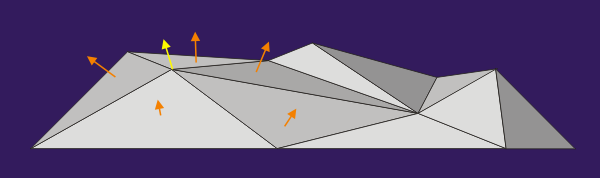
Im Zusammenhang mit der Beleuchtung gibt es eine weitere Anwendung, die auf einer besonderen Art von Normalen beruht. Anstatt die Flächennormale eines Polygons zu übergeben, kann man jedem Vertex eine eigene Normale mit auf den Weg geben. Bei entsprechender Ausrichtung dieser Vertexnormalen wird das Licht so verteilt, dass der optische Eindruck von abgerundeten Ecken und Kanten entsteht (smoth shading).

Die Richtung einer Vertexnormalen ergibt sich aus den Flächennormalen aller angrenzenden Polygone. Die Vertexnormale gibt eine "mittlere" Richtung an. Zur Berechnung werden alle betroffenen Flächennormale addiert und das Ergebnis wieder normalisiert.

Vertexnormale werden vorzugsweise zur Darstellung des Terrains gebraucht, seltener zur Darstellung von Objekten, wo häufig die scheinbaren Abrundungen stören. Zweckmäßigerweise berechnet man die Vertex-Koordinaten sowie die Vertexnormalen aller Terrain-Dreiecke im voraus und speichert sie in einem Vertex-Array. Das hat außerdem den Vorteil, dass das Terrain in einem Rutsch mit glDrawElements gezeichnet werden kann. Das geht schneller und einfacher als jedes Polygon einzeln zu zeichnen.

Normale und Transformationen

Ein wenig Aufmerksamkeit ist erforderlich, wenn ein Modell transformiert werden soll. glTranslate und glRotate sind problemlos, da diese Transformationen keinen Einfluss auf die Länge der Normalen haben. Anders verhält es sich mit glScale. Die Normale hat danach nicht mehr die Länge 1, wodurch bei stärkeren Abweichungen unerwartete Beleuchtungsverhältnisse entstehen können. In diesem Fall sollte die interne Normalisierung mit glEnable(GL_NORMALIZE) aktiviert sein. Im "OpenGL Programming Guide" wird aber darauf hingewiesen, dass dadurch der Grafikprozessor deutlich beansprucht wird. Schneller ist die Alternative glEnable(GL_RESCALE_NORMAL), die jedoch nur in Frage kommt, wenn in den drei Dimensionen mit dem gleichen Faktor skaliert wird.

Als Ausweg aus dem "Scale-Dilemma" bietet sich an, die Modelle vorher zu skalieren. Wenn in den drei Dimensionen unterschiedlich skaliert wird, müssen danach alle Normalen des Modells neu berechnet werden, da sie eine andere Richtung erhalten.