Definition

Das Skalarprodukt zweier Vektoren ist das Produkt aus den Beträgen (Längen) der beiden Vektoren sowie dem Cosinus des von den Vektoren eingeschlossenen Winkels:

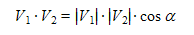
Das Ergebnis ist kein Vektor, sondern ein skalarer Wert (daher der Name). Das Skalarprodukt wird üblicherweise mit einem Multiplikationspunkt zwischen den beiden Vektoren notiert.

Skalarprodukt von Einheitsvektoren

Das Skalarprodukt aus zwei Einheitsvektoren (normalisierten Vektoren) hat eine besondere Bedeutung. Weil die Länge beider Vektoren 1 ist, reduziert sich das Skalarprodukt auf den Cosinus des Winkels:

Damit wird die Information über den Richtungsunterschied der beiden Vektoren herausgefiltert. Entsprechend der Cosinusfunktion liegt das Ergebnis im Intervall [-1 ... +1]. Einige typische Fälle:

Eigenschaften

Das Skalarprodukt ist symmetrisch, d.h. es gilt:

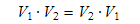
Die Reihenfolge, in der die beiden Vektoren als Funktionsparameter übergeben werden, spielt demnach keine Rolle. Ferner ist das Skalarprodukt distributiv, wenn es mit Vektoradditionen verknüpft wird:

Schließlich bleibt noch zu erwähnen, dass das Skalarprodukt nicht assoziativ ist, denn das Ergebnis ist eine skalare (reele) Zahl, die nicht mit einem Vektor zu einem neuen Skalarprodukt verknüpft werden kann. Darüber hinaus ergibt es sachlich keinen Sinn, aus mehr als zwei Vektoren ein Skalarprodukt zu errechnen. Wie soll z.B. der Winkel zwischen drei Vektoren definiert werden?

Skalarprodukt in Komponentenschreibweise

In der 3D-Programmierung werden Vektoren üblicherweise in der Komponentenform notiert und gespeichert. Damit lässt sich das Skalarprodukt berechnen, ohne die Länge der beiden Vektoren zu kennen.

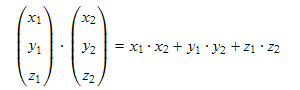
Wenn beide Vektoren normalisiert sind, lässt sich z.B. mit Hilfe von cos^-1 der Winkel zwischen den Vektoren berechnen. Umgekehrt, wenn Vektoren die gleiche Richtung haben (Cosinus = 1), entspricht das Ergebnis dem Produkt der beiden Vektorlängen.

Funktion zur Berechnung des Skalarproduktes

double DotProduct (TVector v1, TVector v2)
{
    return v1.x * v2.x + v1.y * v2.y + v1.z * v2.z;
}

Anwendungen in 3D-Programmen

Die Berechnung des Skalarproduktes gehört zu den am häufigsten angewandten Vektoroperationen. Insbesondere die Richtungsaussage spielt dabei häufig eine Rolle. Deshalb ist in diesen Fällen streng darauf zu achten, dass die Vektoren normalisiert sind. Die Anwendungsmöglichkeiten sind so vielfältig, dass hier nur einige Beispiele genannt werden können:

• Richtungsvergleiche (z.B. Bewegungsrichtung und Ausrichtung eines Hindernisses)
• Abstands- und Positionsberechnungen, insbesondere in Verbindung mit Ebenen
• Projektion von Vektoren auf Ebenen (Zerlegung von Vektoren)
• Intersektionsberechnungen verschiedenster Art
• ...

Das Skalarprodukt hat nicht nur Bedeutung in geometrischen Zusammenhängen. Bekannt ist z.B. die physikalische Definition von Arbeit als Produkt aus Kraft und Weg (W = F * s). In 3D-Programmen könnte diese Beziehung evtl. im Zusammenhang mit physikalischen Simulationen bedeutsam werden. Häufig werden für F und s keine Vektoren benutzt, sondern reele Zahlen. Unter der Voraussetzung, dass Kraft und Weg die gleiche Richtung haben, ist das in Ordnung. Tatsächlich weichen die beiden Richtungen in der Realität meistens voneinander ab, und nur die gemeinsamen Richtungsanteile werden für die physikalische Arbeit wirksam. Die gemeinsamen Richtungsanteile sind definiert als das Skalarprodukt der beiden Vektoren. Das Höchstmaß an Arbeit wird bei gleicher Richtung erzielt, dann ist der Cosinus = 1.