Erklärung

Zwei oder mehr Vektoren werden addiert, indem sie einfach aneinander gehängt werden. Ein Vektor wird von einem andern Vektor subtrahiert, indem der Umkehrvektor addiert wird.

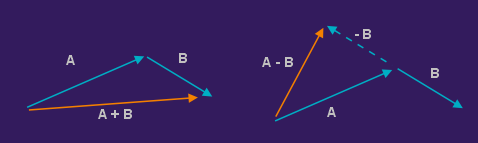
Abgesehen von den Sonderfällen, wo die beiden Ursprungsvektoren die gleiche oder entgegengesetzte Richtung haben, lässt sich folgendes feststellen: Die Richtung des resultierenden Vektors weicht von der Richtung der ursprünglichen Vektoren ab. Ebenso ist der Ergebnisvektor kürzer als die beiden ursprünglichen Vektoren zusammen.

Analogien und Eigenschaften

Bezüglich der Eigenschaften gibt es eine Reihe von Analogien im elementaren Zahlenbereich. Eine Analogie wurde bereits erwähnt, nämlich der Zusammenhang von Subtraktion und Addition: A - B = A + (- B). Außerdem:

• Es existiert ein neutrales Element, für das gilt: A + 0 = A. Die Null hat ihre Entsprechung im Nullvektor; das ist ein Vektor der Länge 0 und ohne definierte Richtung.
• Die Addition ist kommutativ, so dass gilt: A + B = B + A. Das lässt sich im Fall der Vektoraddition zeichnerisch leicht überprüfen.
• Die Addition ist assoziativ, es können also beliebige Teilsummen gebildet werden: A + (B + C) = (A + B) + C. Auch das ist zeichnerisch schnell nachzuprüfen.

Berechnung der Vektorsumme

Ebenso trivial wie die zeichnerische Vektoraddition ist die rechnerische Lösung: Die einzelnen Komponenten werden einfach addiert:

Anwendungen

Vektoradditionen und -subtraktionen sind sehr elementare Operationen; infolgedessen greifen viele Vorgänge oder Funktionen darauf zurück.

• Vektoradditionen gibt es z.B. beim Bewegungsablauf von Objekten. Der Weg ist letztlich eine Kette von mehr oder weniger kleinen Wegvektoren.
• Die Subtraktion von Vektoren wird häufig angewandt, um die Differenz zwischen zwei Punkten zu bestimmen. Zwar werden Punkte mit ortsbezogenen Koordinaten anders interpretiert als frei verschiebbare Vektoren, doch formal handelt es sich bei Punkten ebenfalls um Vektoren. Die Differenz ist dann ein "echter" Vektor. Typisches Beispiel ist die Dreiecksseite, die als Vektor, also als Differenz zweier Eckpunkte, dargestellt werden kann. Der Vektor wird u.a. für die Berechnung der Normalen benötigt.

Exkurs: Projektion als Beispiel für die Zerlegung von Vektoren

Wenn ein Vektor (oder eine Zahl) in zwei Summanden zerlegt werden soll, gibt es nur dann eine eindeutige Lösung, wenn einer der Summanden bekannt ist. Die Umformung führt zu einer Subtraktion:

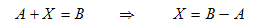
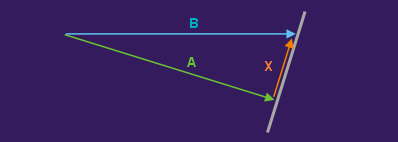
Der Sachverhalt wird z.B. bei der Projektion eines Vektors auf eine Ebene angewandt. Gegeben ist ein Summenvektor B, der in zwei Teilvektoren zerlegt werden soll, und zwar so, dass einer der beiden Teilvektoren (X) parallel zur Ebene liegt, während der zweite Teilvektor (A) senkrecht auf der Ebene steht. Dieser wird zuerst berechnet; der andere ist das Ergebnis einer Vektorsubtraktion.

Die Projektion spielt bei physikalischen Simulationen eine wichtige Rolle (Zerlegung von Kräften), aber auch, wenn es um die Ausrichtung von Objekten geht (Auswertung des Up-Vektors). Hier eine Funktion:

void ProjectToPlane (TVector planenml, TVector v,
        TVector & parallel, TVector & perpendicular)
{
    // planenml (Normale der Ebene) muss normalisiert sein
    double dotprod = DotProduct (planenml, v);
    perpendicular = ScaleVec (dotprod, planenml);
    parallel = SubtractVectors (v, perpendicular);
}