Erklärung

Unter der Skalierung von Vektoren versteht man die Multiplikation eines Vektors mit einer Zahl. Das Ergebnis ist wieder ein Vektor. Diese Operation beeinflusst die Länge des Vektors, während seine Richtung im Prinzip erhalten bleibt. Ausnahme: Bei der Multiplikation mit einer negativen Zahl erhält der Vektor genau die entgegengesetzte Richtung. (Eine weitere Ausnahme ist die Skalierung mit unterschiedlichen Faktoren; dabei kann der Vektor ebenfalls eine andere Richtung erhalten. Siehe Abschnitt unten.)

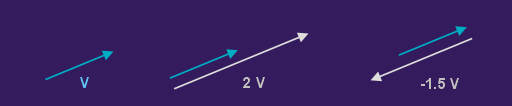
Sonderfälle

• Durch die Multiplikation mit 0 entsteht ein Nullvektor, der keine definierte Richtung hat und praktisch unbrauchbar ist.
• Die Multiplikation mit -1 dreht den Vektor in die umgekehrte Richtung.
• Die Division durch die Länge des Vektors macht einen Einheitsvektor daraus (normalisiert den Vektor).

Rechenvorgang

Beim Skalieren eines Vektors werden die einzelnen Komponenten mit dem Skalierungsfaktor multipliziert:

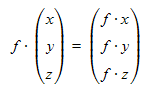
Anwendung

Die Skalierung von Vektoren kommt in vielen Situationen vor. Einige Beispiele:

Ausgleich unterschiedlicher Zeitspannen. Die Zeitspanne von Frame zu Frame kann erheblich schwanken und auch von Computer zu Computer unterschiedlich sein. Um gleichmäßige, kontrollierte Bewegungen zu erzeugen, werden die betroffenen Vektoren, meistens Wegstrecken oder Kräfte, mit der Zeitspanne multipliziert.

Justierung von Kräften. Wenn mehrere Kräfte auf ein Objekt wirken, müssen sie vor der Addition zu einer resultierenden Kraft aufeinander abgestimmt werden. Dazu wird jede einzelne Kraft mit einem passenden Faktor skaliert.

Normalisierung von Vektoren. Viele Rechnungen verlangen einen normalisierten Vektor, also einen Vektor mit der Länge 1. Dazu wird der Vektor durch seine Länge dividiert. Häufig kommt es vor, dass der normalisierte Vektor nach seiner Bearbeitung wieder auf die ursprüngliche Länge zurückskaliert werden muss. In solchen Fällen sollte man die bei der Normalisierung berechnete Länge zwischenspeichern.

Skalierung von Objekten. Nicht immer ist es günstig (oder möglich), die Skalierung mit glScale von OpenGL durchführen zu lassen. Wenn man selber ein Objekt skaliert, werden alle Vertices mit dem gewünschten Faktor multipliziert. Die Vertices sind zwar Punkte, werden aber rechnerisch wie Vektoren behandelt.

Skalierung mit unterschiedlichen Faktoren

Im Normalfall werden, wie oben beschrieben, die Vektorkomponenten mit dem selben Faktor multipliziert. Das muss nicht immer so sein. In bestimmten Situationen, z.B. bei der Skalierung von Objekten, können für x, y und z verschiedene Faktoren verwendet werden. Eigentlich ist das ein typischer Fall für eine Matrix und lässt sich am besten mit einer Matrix beschreiben:

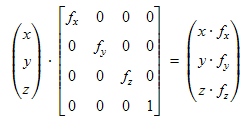
Für die Berechnung muss aber nicht unbedingt eine Matrix herangezogen werden. Mitunter geht es einfacher und schneller, wenn die Komponenten einzeln multipliziert werden. Der Vektor erhält dadurch eine andere Länge und eine andere Richtung, von Sonderfällen abgesehen.