Geodreieck und Matrizen, eine Analogie

Mit diesem Tutorial möchte ich vor allem Anfängern unter die Arme greifen, die ihre allerersten Schritte in OpenGL machen. Ich glaube, jeder Anfänger tut sich schwer mit den Befehlen glTranslate, glRotate und glScale. Selbst bei den schon etwas Fortgeschrittenen scheint es noch das eine oder andere Missverständnis zu geben. Sicher, man lernt recht schnell, mit den Dingen richtig umzugehen, dafür gibt es ja erprobte Regeln. Doch ob man die Zusammenhänge auch richtig durchschaut, ist eine andere Sache.

Woran liegt es, dass wir am Anfang solche Probleme mit diesen Befehlen haben? Ich denke, das liegt einmal an den Missverständnissen, die immer wieder kursieren und auf Halbwahrheiten beruhen. Es liegt aber auch daran, dass wir uns die Situation nicht ganz leicht vorstellen können. Auf die Missverständnisse werde ich im Folgetutorial eingehen, und was die Vorstellung betrifft, so soll dieses Tutorial einen Beitrag leisten.

Als ich meine ersten Gehversuche mit OpenGL unternahm, war ich beeindruckt von dem, was Matrizen in OpenGL leisten. Was eine solche Matrix genau ist und vor allem was exakt ihre Funktion ist, davon hatte ich nur eine verschwommene Vorstellung. "Verschiebungen und Rotationen werden in Matrizen gespeichert", las ich irgendwo. Schön, dachte ich, da wird also ein Punkt verschoben, in einer Matrix gespeichert, und am Schluss formt OpenGL aus allen Matrizen ein Bild.

Erst als ich merkte, dass diese Vorstellung überhaupt nicht zu den Ergebnissen auf dem Bildschirm passen wollte, stellte ich mein Verständnis von Matrizen auf den Prüfstand und kam nach und nach zu der Erkenntnis, dass wohl etwas ganz anderes dahinter stecken müsste. Endgültig klar wurde die Sache, als ich erfuhr, dass für das Zeichnen von Szenerien genau eine Matrix zuständig ist, nämlich die Modelview-Matrix. Ein einziges Array von genau 16 Zahlen. Da machte es endgültig klick: die Matrix kann lediglich ein Werkzeug sein, um die Szenerie zu zeichnen, eine Art Schablone.

Werkzeug zum Zeichnen? Das benutzen wir doch auch, wenn wir etwas aufs Papier bringen wollen. Ein Lineal zum Beispiel, oder ein Geodreick. Und in der Tat, beim Vergleich eines Lineals oder Geodreiecks mit einer OpenGL-Matrix stellen sich verblüffende Gemeinsamkeiten heraus. Allerdings gilt das nur bis zu einem gewsissen Grad, alles lässt sich damit nicht veranschaulichen. Aber es reicht, um die Befehle glTranslate und glRotate mit ihren Tücken zu verstehen. Beginnen wir also mit dem Zeichnen ...

Verschiebungen - glTranslate

Wir nehmen ein großes Blatt Papier, vielleicht einen Bogen Packpapier, breiten es auf dem Tisch aus und markieren in der Mitte einen großen, roten Punkt. Das ist der Punkt, an dem sich alles orientiert, der Nullpunkt des Welt-Koordinatensystems. In Gedanken legen wir das Koordinatensytem als Gitter darüber.
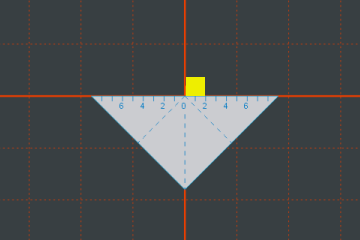Bevor mit zeichnen, legen wir das Geodreieck in der Mitte an und richten es aus. Damit haben wir ein glLoadIdentity durchgeführt. Zuerst zeichnen wir die Grundlinie mit den Punkten (0, 0) und (2, 0). Die beiden oberen Punkte lassen sich leicht ergänzen. Vielleicht noch erwähnenswert: Der linke, untere Punkt ist der Drehpunkt des Quadrates, weil er im Mittelpunkt des Koordinatensystems liegt.

Das Zeichnen des Quadrates entspricht den 4 Vertexangaben zwischen glBegin (GL_QUADS) und glEnd.
Im nächsten Schritt zeichnen wir ein Quadrat, dass um 6 Einheiten nach rechts verschoben ist (6 Einheiten in pos. x-Richtung). Wie man sieht, können wir das Geodreieck liegen lassen und brauchen nur ein wenig zu rechnen.

In OpenGL können wir ähnlich verfahren, indem wir die Vertices nach wie vor auf den Welt-Nullpunkt beziehen. Die Eckpunkte des Quadrates (Vertices) haben die Koordinaten (6, 0), (8, 0) (8, 2) und (8, 6).
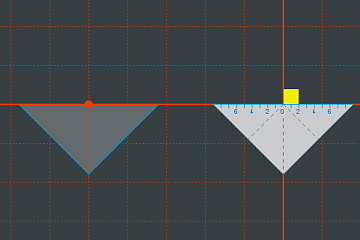Doch es gibt noch eine andere Möglichkeit. Wir können das Geodreieck an die gewünschte Stelle schieben und damit wieder auf die Eckpunkte 0 und 2 zurückgreifen.

Dem Verschieben des Geodreicks entspricht in OpenGL der Befehl glTranslate. glTranslate erzeugt eine Verschiebungsmatrix.

An dieser Stelle sollten wir kurz anhalten und uns einige Dinge klarmachen. Das Geodreieck verkörpert ja so etwas wie ein eigenes Koordinatensystem, mit dem Nullpunkt an der bekannten Stelle in der Mitte der Hypotenuse. Wenn wir das Geodreieck verschieben, nehmen wir das (lokale) Koordinatensystem mit und plazieren es an irgendeiner Stelle im globalen Weltkoordinatensystem. Alle nun folgenden Zeichenbefehle beziehen sich auf das lokale Koordinatensystem und sind damit von der vorangegangenen Verschiebung betroffen.

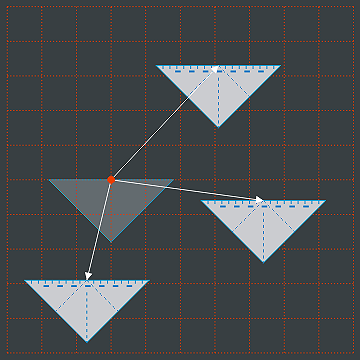Das Verschieben kann in allen Richtungen erfolgen, doch dabei ist zu beachten, dass die Lage des Geodreiecks immer gleich bleibt. Es ist also eine typische Parallelverschiebung.
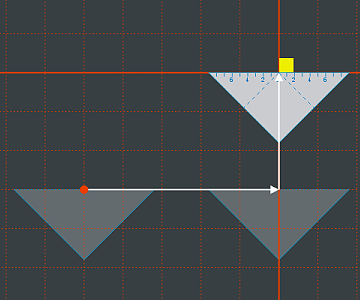Die Verschiebung kann in mehreren Schritten erfolgen. Hier wurde zuerst um 5 Einheiten nach rechts, dann um 3 Einheiten nach oben verschoben.

Wenn wir das Geodreieck mehrmals nacheinander verschieben, müssen wir nicht jedesmal erst zum Weltmittelpunkt zurück, sondern wir können das Dreieck zuerst irgendwo hinschieben, dort zeichnen, dann weiter verschieben, erneut zeichnen usw.

In OpenGL ist es ähnlich. Jede Matrix baut auf der vorangegangenen auf; alle Verschiebungen beziehen sich auf die zuletzt verwendete Matrix - solange, bis glLoadItentity durchgeführt wird, dann geht's zurück zur Mitte

Rotationen - glRotate

Als nächstes wollen wir das schon vertraute Quadrat rotieren, also untersuchen, wie das mit glRotate ist. Dazu gehen wir wieder in die Mitte zurück (glLoadIdentity).

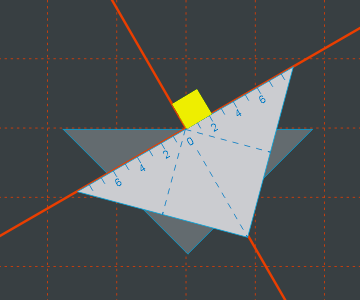Nun drehen wird das Geodreieck und zeichen wie gewohnt: (0, 0), (2, 0) usw. Wie beim Verschieben entsteht ein neues, lokales Koordinatensystem, diesmal mit gedrehten Achsen.
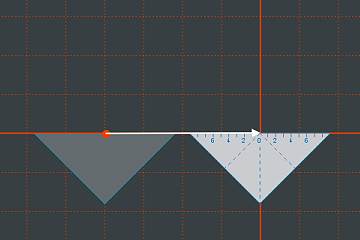Um das Quadrat an anderer Stelle gedreht zu zeichnen, gehen wir in zwei Schritten vor. Zuerst verschieben wir das Geodreieck ...
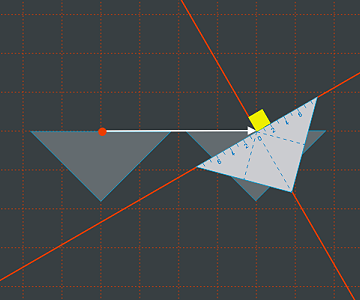... dann drehen wir es in die gewünschte Richtung - und zeichnen. Das Resultat ist so wie es sein soll.
Wir können natürlich auch auf den Gedanken kommen, das Geodreieck zuerst zu drehen ...
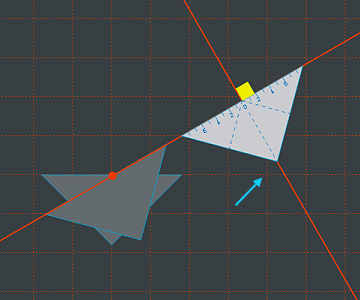... und dann zu verschieben.

Doch hoppla, da sollte das Quadrat doch gar nicht hin. Der blaue Pfeil zeigt die verfehlte Position.

Wenn in OpenGL ein Objekt nur um seine eigene Achse und nicht um einen entfernt liegenden Punkt gedreht werden soll, gilt die Regel, dass zuerst glTranslate und dann glRotate durchgeführt wird.

Skalierungen - glScale

Wie glTranslate und glRotate ist auch glScale ein zwar nützlicher, aber nicht unbedingt erforderlicher Befehl. Wir können ein Objekt ohne glScale in beliebiger Größe zeichnen, indem wir die Vertices entsprechend anpassen. Um das Quadrat mit halber Größe zu zeichnen, würden wir nicht mehr mit den Koordinaten 0 und 2, sondern mit den Koordinaten 0 und 1 oder auch -0.5 und +0.5 arbeiten. Oder wir verwenden in der Vertexliste Variablen und können dieselbe Zeichenfunktion für beliebige Objektgrößen benutzen. glScale kann die Sache aber vereinfachen. Im folgenden geht es immer um den Skalierungsfaktor 0.5; das Quadrat soll in halber Größe gezeichnet werden.

Um diese Halbierung mit dem Geodreieck nachzuvollziehen, nehmen wir einfach ein kleineres Dreieck, dass außerdem eine engere Skala hat.

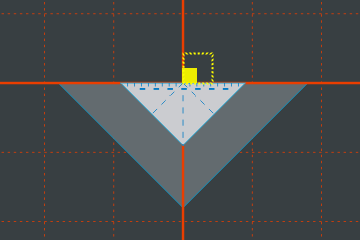Hier wird das Quadrat mit den gewohnten Koordinaten 0 und 2 im Welt-Nullpunkt gezeichnet. Es erscheint halb so groß wie bisher.
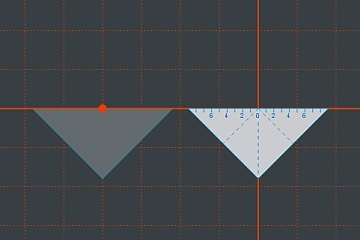Im nächsten Schritt verschieben wir zunächst das normale Geodreieck ...
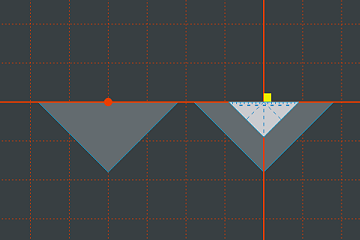... und ersetzen es dann durch das Dreieck mit der feineren Skala. Kein Problem, das Ergebnis ist so, wie wir es wollten.
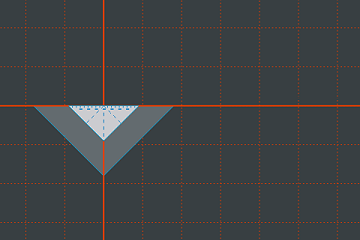Erneut vertauschen wir die Reihenfolge der beiden Aktionen. Wir skalieren zunächst ...
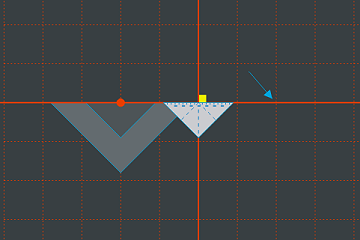... und verschieben anschließend.

Hoppla, das Quadrat sollte doch weiter verschoben werden! Wenn in OpenGL nur der Gegenstand skaliert werden soll, nicht aber der Verschiebemaßstab, muss zuerst verschoben und dann skaliert werden.

Damit dürfte nun klar sein, warum wir zum Zeichnen von Objekten in OpenGL zuerst glTranslate bemühen und anschließend glRotate bzw. glScale. Doch wie verhält es sich mit der Reihenfolge von glRotate und glScale? Gibt es hierbei auch Regeln, die einzuhalten sind? Sofern wir in allen drei Dimensionen die gleiche Skalierung benutzen, kann das Geodreieck die Frage beantworten. Aber ...

Die Grenzen des Geodreiecks

Wenn wir glScale mit unterschiedlichen Skalierungsfaktoren aufrufen, dann kann uns das Geodreick keine Anschauungshilfe mehr geben. Es ist dafür nicht mehr geeignet, denn es müsste mit zwei verschiedenen Skalen ausgestattet sein. Überhaupt ist die unterschiedliche Skalierung eine Angelegenheit, die manche Tücke in sich birgt. Es beginnt schon beim Koordinatensystem; das Gitternetz besteht nicht mehr aus Quadraten, sondern aus Rechtecken. Das hat u.a. zur Folge, dass sich die Winkel verschieben.

Highlight ist die unterschiedliche Skalierung in Verbindung mit einer Rotation. Nur als Gedankenexperiment: Was geschieht, wenn wir zuerst skalieren, dann rotieren? Der Punkt wird nicht mehr auf einer Kreisbahn um den Koordinatennullpunkt gedreht, sondern auf einer elliptischen Bahn. Im dreidimensionalen Raum tritt ein Ellipsoid an die Stelle der Kugel. Das sind Rotationen, mit der wir uns nur schlecht anfreunden können, denn beim Drehen wird die Form verändert. Umgekehrt sieht's etwas freundlicher aus. Wenn wir zuerst drehen und dann skalieren, gibt's nur die Spreizung.

Das soll erst mal reichen. Ich denke, wenn wir ein Gespür dafür bekommen haben, wie bei jeder Aktion ein neues Koordinatensystem entsteht, dass in das vorherige eingebettet ist, dürfte es nicht mehr allzu schwer fallen, die Transformationsbefehle glTranslate, glRotate und glScale durchdacht anzuwenden. Im zweiten Teil des Tutorials geht es im Prinzip um die gleiche Thematik, aber mit anderen Schwerpunkten. Dann rückt die Matrix in den Vordergrund.