Der Raumwinkel
Der Raumwinkel ist für viele eine geheimnisvolle oder missverstandene Größe. Missverstanden deshalb, weil der herkömmliche Winkelbegriff nicht ohne weiteres funktioniert. In der Photometrie hat der Raumwinkel eine relativ große Bedeutung. Deshalb, und weil man ihn nicht einfach so zwischendurch erklären kann, behandle ich ihn in diesem speziellen Beitrag.
Was bedeutet der Raumwinkel?
Machen wir in Gedanken ein kleines Experiment. Wir nehmen eine Taschenlampe, und zwar eine herkömmliche Stablampe, mit einem kleinem Glühbirnchen und einem Hohlspiegel, der sich verstellen lässt. Die Lampe sendet einen Lichtkegel aus, der an der Wand eine mehr oder weniger große, mehr oder weniger kreisrunde Fläche beleuchtet, und das in aller Regel ungleichmäßig.
Aber diese Unvollkommenheiten sollen keine Rolle spielen, entscheidend ist der Begriff Lichtkegel. Wenn wir nämlich den Reflektor verstellen, dann können wir z.B. erreichen, dass der Lichtkegel enger wird, gleichzeitig die beleuchtete Stelle an der Wand heller. Wir konzentrieren also die Lichtleistung auf eine kleinere Fläche. Um genau diese Zusammenhänge zwischen der Weite eines Lichtkegels und der davon abhängigen Lichtleistung geht es beim Raumwinkel.
Nun etwas genauer
Wir machen nun ein weiteres Experiment, das genauere Aufschlüsse erlaubt als der ungleichmäßge Schein der Taschenlampe. Wir nehmen einen normalen Diaprojektor, der mit einem Zoomobjektiv ausgestattet ist, und stellen ihn 2 m vor einer Wand auf. Als Dia wählen wir ein 5x5 cm großes Pappquadrat, in dessen Mitte wir ein Loch von einigen Millemetern Durchmesser stanzen. Wir stellen den hellen Kreis an der Wand nun scharf und messen dessen Durchmesser, vielleicht 15 cm (A).
Nun erhöhen wir den Abstand r auf 4 m, stellen erneut scharf und messen wieder (B). Ok, es dürfte nicht überraschen, dass der Leuchtkreis nun etwa den doppelten Durchmesser hat. Intuitive Anwendung des Strahlensatzes. Dass durch die Neufokussierung die Verhältnisse ein klein wenig verschoben sind, ignorieren wir mal. Und natürlich ist der größere Kreis nun dunkler, ebenfalls wie erwartet.
Dann gehen wir hin und verstellen das Zoomobjektiv so, dass sich wieder die ursprüngliche Kreisgröße (15 cm oder was auch immer wir am Anfang hatten) ergibt, gleichzeitig aber auch die ursprüngliche Helligkeit (C). Was sich gegenüber der ersten Einstellung geändert hat, dass ist offenbar der Winkel des Lichtkegels, der nun kleiner geworden ist, und natürlich der Abstand, den wir verdoppelt haben. Genau das sind die beiden Komponenten, die den Raumwinkel ausmachen.
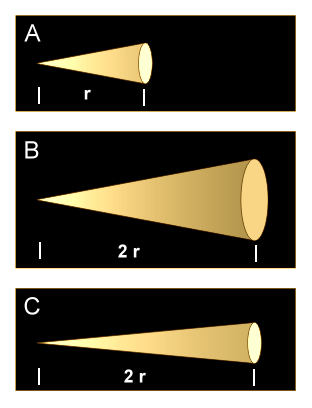
Der Raumwinkel
Beim Raumwinkel geht es also darum, wie stark das von der Lichtquelle ausgehende Licht gebündelt wird, oder - anders herum - wie intensiv das Licht in einem bestimmten Bündel ist. Die Situationen A und B im Bild oben repräsentieren den gleichen Raumwinkel, während C wegen der stärkeren Bündelung einen kleineren Raumwinkel darstellt. Doch wie wird der Raumwinkel genau erfasst? Der Winkel an der Spitze ist nicht geeignet, weil das Bündel ja irgendeine Form haben kann, z.B. eine Ellipse.
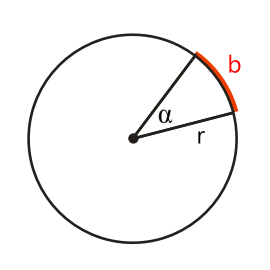
Wenn wir uns noch einmal den gewohnten Winkel auf einer ebenen Fläche vor Augen führen, dann fällt uns sicher ein, dass wir den Winkel α gar nicht direkt messen müssen, denn wir können ja auch den Kreisbogen b heranziehen. Der hängt zwar vom Radius r ab, aber proportional. D.h. bei doppeltem Radius erhalten wir die doppelte Bogenlänge usw. Wenn wir demnach die Bogenlänge durch den Radius dividieren, was zum Einheitskreis mit r = 1 führt, bekommen wir ein eindeutiges Maß für den Winkel.
Wenn α = 360° beträgt, ist die Bogenlänge gleich dem Umfang des Kreises, also b = 2 π r. Im Einheitskreis wäre das 2 π = 6.28.
Wenn wir nun diese Zusammenhänge in den 3-dimensionalen Raum übertragen, gelangen wir zum Raumwinkel. An die Stelle des Kreises tritt nun eine Kugel, anstelle des Kreisbogens verwenden wir nun die Fläche A, die einen Teil der Kugeloberfläche ausmacht. Und natürlich kommt der Radius wieder ins Spiel, aber der Zusammenhang zwischen Radius und Winkel ist nun ein etwas anderer. Wenn wir den Radius verdoppeln, vervierfacht sich die Fläche auf der Kugel, bei dreifachem Radius ist sie 9 mal so groß. Die Fläche ist demnach proportional zum Quadrat des Radius, und um die Fläche auf eine Einheitskugel mit r = 1 umzurechnen, muss sie durch r2 dividiert werden.
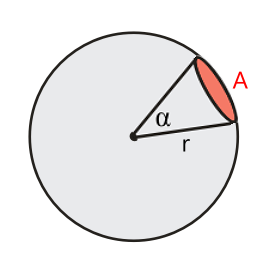
Erneut stellt sich die Frage, wie groß der Raumwinkel ist, wenn die gesamte Kugeloberfläche erfasst wird. Nun, für die Kugeloberfläche gilt O = 4 π r2, in der Einheitskugel wäre das das A =12.57.
Das Maß für den Raumwinkel
An und für sich hat der Raumwinkel keine physikalische Dimension und demnach keine Benennung, die sich aus einem Einheitensystem ableiten ließe. So hat man einfach eine Maßeinheit festgelegt: 1 Steradiant (sr). Das ist die Fläche von 1 m2 auf der Oberfläche einer Kugel mit r = 1 m (oder auch alles in cm). Eine Lichtquelle, die rundum strahlen kann, sendet ihr Licht in einen Raumwinkel von 12.57 sr (siehe oben).
Übrigens haben wir auch bei der Maßeinheit eine Analogie zwischen Flächenwinkel und Raumwinkel. Die Bogenlänge im Einheitskreis wird als Radiant (rad) bezeichnet, womit sich für den Vollkreis ein Winkel von 2 π rad = 6.28 rad ergibt.
